The story of the Smartarduino Doit 6Dof Robotic Arm - Part 3

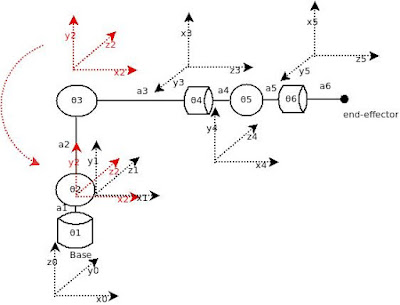
This kinematic diagram looks like the DoIT robot with a very important omission. The DoIT is a 'stacking robot' that preserves the orientation of the spherical wrist (the three last links and the end-effector) when θ₁ (Servo-1) is moved.

There's an excellent paper on it here.

For this kinematic diagram to be usable, every time we change θ₁, we must change θ₂ by the same amount in the opposite direction.

I will be trying to find the Denavit-Hartenberg parameters, but not before I've found all the rotation and displacement matrices. D-H is simpler to use but doesn't offer as much insight.

Let's start by reminding ourselves of the rotation matrices

• Around x
  
• Around y
  
• Around z
  

Now, let's take a long, hard look at that kinematic diagram because there's something wrong with it. The numbering of the angles is supposed to indicate what frame is affected by the rotation. Therefore, the first angle is θ₁ because it rotates frame 1. But, there's more:

X₂ does not intersect Z₁.

To fix this, we renumber the angle and move Frame(2) down so it sits on top of Frame(1).

Now, angles are numbered correctly, and X₂ intersects Z₁

It might seem weird to just move stuff around like this, but think about it: By moving stuff about, we're changing its location, not its orientation.

We will be affecting the displacement vectors, but not the rotation matrices.

Ponimayet?

The rotation matrix R⁰₁ consists of two parts, one due to the way the links are bolted together with the servos in resting position, and one due to the way the servo rotates the joint. We have to dot-multiply them together in order to find the complete rotation matrix for the joint.

We'll take the one with the servos in resting position first.

To find the rotation from Frame(0) to Frame(1), let's see how the axes of Frame(1) are projected onto the axes of Frame(0) and set up a matrix.

The first column shows the projection of X₁onto the axes X₀, Y₀, and Z₀, respectively. It is in the same direction as X₀, so its projection will be 1.

The other axes (Y₀ and Z₀) are perpendicular to X₁ and so its projections onto them will both be 0. We're done with the first column.

The second column is for Y₁. It is in the same direction as Z₀, and perpendicular to the two others, so we get

As one might have guessed, the third column is for the Z₁ axis.
The finished matrix looks like this:

And our complete rotation matrix from 0 to 1 looks like this:

To calculate: Drink coffee. Drink RedBull. This is error-prone and tedious. Thank Zuse we have computers.

It looks a lot better when I don't show how it's done. Besides, since most entries in the matrix on the left are zero, multiplying them is a lot simpler than it looks.

Um ... wait. Did I multiply those in the correct order? Nevermind. Let's move on.

Now, we proceed to find R⁰₆=R⁰₁·R¹₂·R²₃·R³₄·R⁴₅·R⁵₆. Same procedure as above, but this time, I'll try to recap the rules as I go.